Question

Prove that |a| < b if and only if -b < a < b

Answer 1

Since,

`|x|=\left\{\begin{matrix}x &\text{ if } x \geq 0 \\ -x &\text{ if } x < 0\end{matrix}\right.`

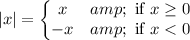
Here, the given equation is,

|a| < b

Case 1 : if a ≥ 0,

|a| < b ⇒ a < b

Case 2 : If a < 0,

|a| < b ⇒ -a < b ⇒ a > - b

( Since, when we multiply both sides of inequality by negative number then the sign of inequality is reversed. )

|a| < b ⇒ a < b or a > - b ⇒ -b < a < b

Conversely,

If -b < a < b

⇒ a < b or a > - b

⇒ a < b or -a < b

⇒ |a| < b

Hence, proved..