Question

An electron is released from rest at the negative plate of a parallel plate capacitor. The charge per unit area on each plate is = 2.1 × 10^-7 C/m^2, and the plates are separated by a distance of 1.2 × 10^-2 m. How fast is the electron moving just before it reaches the positive plate?

Answer 1

Step-by-step explanation:

An electron is released from rest, u = 0

We know that charge per unit area is called the surface charge density i.e.
`\sigma=(q)/(A)=2.1* 10^(-7)\ C/m^2`

Distance between the plates,
`d=1.2* 10^(-2)\ m`

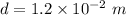
Let E is the electric field,

`E=(\sigma)/(\epsilon_o)`

`E=(2.1* 10^(-7))/(8.85* 10^(-12))`

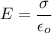
E = 23728.81 N/C

Now,
`ma=qE`

`a=(qE)/(m)`

`a=(1.6* 10^(-19)* 23728.81)/(9.1* 10^(-31))`

`a=4.17* 10^(15)\ m/s^2`

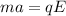
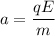
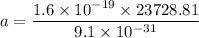
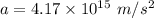
Let v is the speed of the electron just before it reaches the positive plate. So, third equation of motion becomes :

`v^2=2ad`

`v^2=2* 4.17* 10^(15)* 1.2* 10^(-2)`

`v=10.003* 10^6\ m/s`

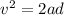
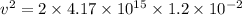
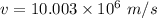
Hence, this is the required solution.