Question

The radii of curvature of a biconvex lens are 4 cm and 15 cm. The lens is in air, its index of refraction is 1.5. An object is at 1 m before the front surface of the lens. Calculate the distance of the image from the back surface of the lens.

Answer 1

-1.19 m

Step-by-step explanation:

R1 = + 4 cm

R2 = - 15 cm

n = 1.5

distance of object, u = - 1 m

let the focal length of the lens is f and the distance of image is v.

use lens makers formula to find the focal length of the lens

`(1)/(f)=\left ( n-1 \right )\left ( (1)/(R_(1))-(1)/(R_(2)) \right )`

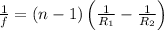
By substituting the values, we get

`(1)/(f)=\left ( 1.5-1 \right )\left ( (1)/(4)+(1)/(15) \right )`

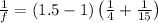
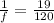`(1)/(f)=(19)/(120)` .... (1)

By using the lens equation

`(1)/(f)=(1)/(v)-(1)/(u)`

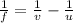
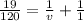`(19)/(120)=(1)/(v)+(1)/(1)` from equation (1)

`(1)/(v)=(19-120)/(120)`

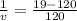
v = -1.19 m