Answer:
Proved
Explanation:
To prove that if n is a perfect square, then n+1 can never be a perfect square
Let n be a perfect square
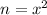
Let
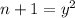
Subtract to get
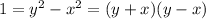
Solution is y+x=y-x=1
This gives x=0
So only 0 and 1 are consecutive integers which are perfect squares
No other integer satisfies y+x=y-x=1