Question

The car starts from rest and accelerates with an acceleration of 2 m/s^2 for 5 s. It then travels at a constant speed for 20 s, before decelerating at -5 m/s^2 until it reaches zero speed. How much distance did the car cover during this journey.

Answer 1

Total distance covered during the journey is 235 m

Solution:

As per the question:

Initial velocity, v = 0 m/s

Acceleration, a =
`2 m/s^(2)`

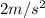
Time, t = 5 s

Now,

For this, we use eqn 2 of motion:

`d = vt + \farc{1}{2}at^(2)`

`d = 0.t + \farc{1}{2}* 2* 5^(2) = 25 m`

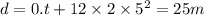
The final speed of car after t = 5 s is given by:

v' = v + at

v' = 0 + 2(5) = 10 m/s

Now, the car travels at constant speed of 10 m/s for t' = 20 s with a = 0:

`d' = vt + \farc{1}{2}at^(2)`

`d' = 10* 20 + \farc{1}{2}* 0* 20^(2) = 25 m`

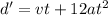
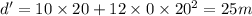
d' = 200 m

Now, the car accelerates at a= - 5
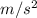`m/s^(2)` until its final speed, v" = 0 m/s:

`v`

`0 = {10}^(2) + 2* (- 5)d`

`100 = 10d`

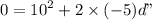
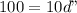
d" = 10 m

Total distance covered = d + d' + d" = 25 + 200 + 10 = 235 m