Answer:
a) $765.13 b) $277,601.23
Explanation:
a) The problem is an example of an ordinary annuity (deposits at the end of the period).
The future value of this type of annuity is:
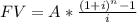
Clearing the annual deposit A
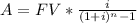
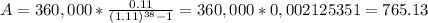
The deposit needed to have $360,000 in 38 years is $765.13
b) We can use the same formula to compute the FV of a known deposit:
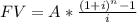
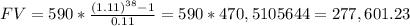
With annual deposits of $590 you will have at 38 years an ammount of $277,601.23