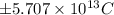Question

The masses of the earth and moon are 5.98 x 1024 and 7.35 x 1022 kg, respectively. Identical amounts of charge are placed on each body, such that the net force (gravitational plus electrical) on each is zero. What is the magnitude of the charge placed on each body?

Answer 1

The magnitude of charge on each is
`5.707* 10^(13) C`

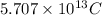
Solution:

As per the question:

Mass of Earth,
`M_(E) = 5.98* 10^(24) kg`

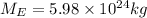
Mass of Moon,
`M_(M) = 7.35* 10^(22) kg`

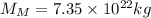
Now,

The gravitational force of attraction between the earth and the moon, if 'd' be the separation distance between them is:

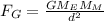`F_(G) = (GM_(E)M_(M))/(d^(2))` (1)

Now,

If an identical charge 'Q' be placed on each, then the Electro static repulsive force is given by:

`F_(E) = (1)/(4\pi\epsilon_(o))(Q^(2))/(d^(2))` (2)

Now, when the net gravitational force is zero, the both the gravitational force and electro static force mut be equal:

Equating eqn (1) and (2):

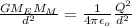
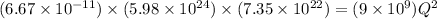
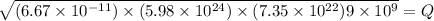
`(GM_(E)M_(M))/(d^(2)) = (1)/(4\pi\epsilon_(o))(Q^(2))/(d^(2))`

`(6.67* 10^(- 11))* (5.98* 10^(24))* (7.35* 10^(22)) = (9* 10^(9)){Q^(2)}`

`\sqrt{\farc{(6.67* 10^(- 11))* (5.98* 10^(24))* (7.35* 10^(22))}{9* 10^(9)}} = Q`

Q =
`\pm 5.707* 10^(13) C`