Answer with Step-by-step explanation:
We are given that sum of three vectors in
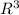 is zero.
is zero.
We have to tell and explain that if sum of three vectors in
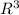 is zero then they must lie in the same plane or not.
is zero then they must lie in the same plane or not.
We know that if three or more vectors lie in the same then they are coplanar.
If three vectors are co-planar then their scalar product is zero.
According to given condition
Let (x,0,0), (-x,0,0) and (0,0,0)
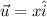
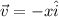
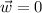
Sum of three vectors=
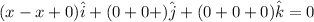
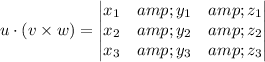
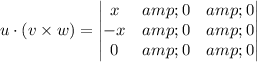
When all elements of one row or column are zero of square matrix A then det(A)=0
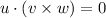
Therefore, vectors u,v and w are co-planar.
Hence, if the sum of three vectors in
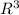 is zero then they must lie in the same plane.
is zero then they must lie in the same plane.