Answers:
a)
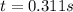
b)
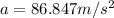
c)
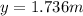
d)
Step-by-step explanation:
For this situation we will use the following equations:
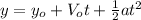 (1)
(1)
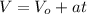 (2)
(2)
Where:
 is the height of the model rocket at a given time
is the height of the model rocket at a given time
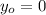 is the initial height of the model rocket
is the initial height of the model rocket
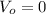 is the initial velocity of the model rocket since it started from rest
is the initial velocity of the model rocket since it started from rest
 is the velocity of the rocket at a given height and time
is the velocity of the rocket at a given height and time
 is the time it takes to the model rocket to reach a certain height
is the time it takes to the model rocket to reach a certain height
 is the constant acceleration due gravity and the rocket's thrust
is the constant acceleration due gravity and the rocket's thrust
a) Time it takes for the rocket to reach the height=4.2 m
The average velocity of a body moving at a constant acceleration is:
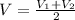 (3)
(3)
For this rocket is:
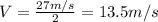 (4)
(4)
Time is determined by:
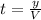 (5)
(5)
 (6)
(6)
Hence:
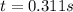 (7)
(7)
b) Magnitude of the rocket's acceleration
Using equation (1), with initial height and velocity equal to zero:
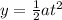 (8)
(8)
We will use
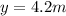 :
:
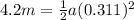 (9)
(9)
Finding
 :
:
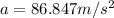 (10)
(10)
c) Height of the rocket 0.20 s after launch
Using again
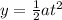 but for
but for
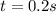 :
:
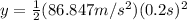 (11)
(11)
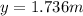 (12)
(12)
d) Speed of the rocket 0.20 s after launch
We will use equation (2) remembering the rocket startted from rest:
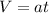 (13)
(13)
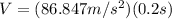 (14)
(14)
Finally:
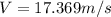 (15)
(15)