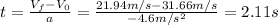Answer:
The minimum time to get the car under max. speed limit of 79 km/h is 2.11 seconds.
Step-by-step explanation:
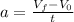
isolating "t" from this equation:
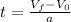
Where:
a=
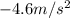 (negative because is decelerating)
(negative because is decelerating)
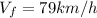
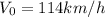
First we must convert velocity from km/h to m/s to be consistent with units.
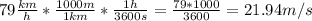
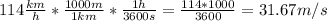
So;