Question

A hot-air balloon is descending at a rate of 1.9 m/s when a passenger drops a camera. If the camera is 47 m above the ground when it is dropped, how much time does it take for the camera to reach the ground? If the camera is 47 m above the ground when it is dropped, what is its velocity just before it lands? Let upward be the positive direction for this problem.

Answer 1

The camera lands in t=2.91s with a velocity:

`v=-30.45m/s`

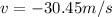
Step-by-step explanation:

The initial velocity of the camera is the same as the hot-air ballon:

`v_(o)=-1.9m/s`

`y_(o)=47m`

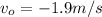
Kinematics equation:

`v(t)=v_(o)-g*t`

`y(t)=y_(o)+v_(o)t-1/2*g*t^(2)`

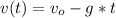
when the camera lands, y=0:

`0=47-1.9t-4.91*t^(2)`

We solve this equation to find t:

t1=-3.29s This solution have not sense in our physical point of view

t2=2.91s

So, the camera lands in t=2.91s

We replace this value in v(t):

`v=v_(o)-g*t=-1.9-9.81*2.91=-30.45m/s`