Question

Aaron finds a pirate’s treasure map. The treasure map says to start at an oak tree and walks 111 feet East and 234 feet South from the tree. How far did the pirate walk? What is the displacement vector for the Pirate? What is the distance and direction relative to East?

Answer 1

pirate walk 259 feet

displacement vector = 111 i - 234 j

direction is along south of east at angle 64.62° , anticlockwise

total travel 345 feet

Step-by-step explanation:

given data

walk east = 111 feet

walk south = 234 feet

to find out

How far did the pirate walk and displacement vector and distance and direction relative to east

solution

we consider here distance AB is 111 feet and than he turn right i.e south distance BC is 234 feet so

so angle BAC will be

tan θ =
`(234)/(111)`

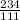
θ = 64.62

and AC distance will be

AC =
`\sqrt{234^(2) + 111^(2)}`

AC = 259 feet

so pirate walk 259 feet

and

displacement vector is express as

displacement vector = AC ( cosθ i + sinθ j )

displacement vector = 259 ( cos64.62 i + sin64.62 j )

displacement vector = 111 i - 234 j

and

so direction is along south of east at angle 64.62° , anticlockwise