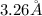Question

What is the associated deBroglie wavelength of a H2 molecule moving on one direction with kinetic energy of (3/2 kT) at 30 K

Answer 1

Answer: The de-Broglie's wavelength of a hydrogen molecule is
`3.26\AA`

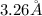
Step-by-step explanation:

Kinetic energy is the measure of temperature of the system.

The equation used to calculate kinetic energy of a particle follows:

`E=(3)/(2)kT`

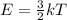
where,

E = kinetic energy of the particles = ?

k = Boltzmann constant =
`1.38* 10^(-23)J/K`

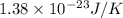
T = temperature of the particle = 30 K

Putting values in above equation, we get:

`E=(3)/(2)* 1.38* 10^(-23)J/K* 30K\\\\E=6.21* 10^(-22)J`

• Calculating the mass of 1 molecule of hydrogen gas:

Conversion factor used: 1 kg = 1000 g

1 mole of hydrogen gas has a mass of 2 grams or
`2* 10^(-3)kg`

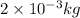
According to mole concept:

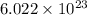`6.022* 10^(23)` number of molecules occupy 1 mole of a gas.

As,
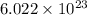`6.022* 10^(23)` number of hydrogen molecules has a mass of
`2* 10^(-3)kg`

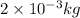
So, 1 molecule of hydrogen will have a mass of =
`(2* 10^(-3)kg)/(6.022* 10^(23))* 1=3.32* 10^(-27)kg`

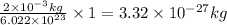
• To calculate the wavelength of a particle, we use the equation given by De-Broglie's wavelength, which is:

`\lambda=(h)/(√(2mE_k))`

where,

`\lambda` = De-Broglie's wavelength = ?

h = Planck's constant =
`6.624* 10^(-34)Js`

m = mass of 1 hydrogen molecule =
`3.32* 10^(-27)kg`

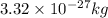
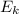`E_k` = kinetic energy of the particle =
`6.21* 10^(-22)J`

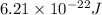
Putting values in above equation, we get:

`\lambda=\frac{6.624* 10^(-34)Js}{\sqrt{2* 3.32* 10^(-27)kg* 6.21* 10^(-22)J}}`

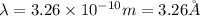`\lambda=3.26* 10^(-10)m=3.26\AA` (Conversion factor:
`1\AA=10^(-10)m` )

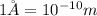Hence, the de-Broglie's wavelength of a hydrogen molecule is
`3.26\AA`