Answer:
At x = 2 and 10.
Explanation:
Given : The cost of producing x hundred items is given by the equation
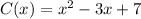
The revenue generated from sales of x hundred units is given by the equation
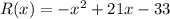
To Find :What values of x will the company break even?
Solution:
Cost function :
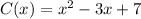
Revenue function :
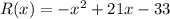
Now to find the company break even :
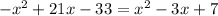
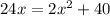
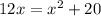
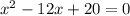
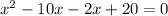
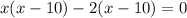
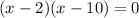
So, x = 2,10
Hence the company break even at x = 2 and 10.