Answer:
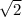 is irrational
is irrational
Step-by-step explanation:
Let us assume that
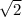 is rational. Thus, it can be expressed in the form of fraction
is rational. Thus, it can be expressed in the form of fraction
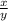 , where x and y are co-prime to each other.
, where x and y are co-prime to each other.
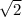 =
=
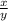
Squaring both sides,
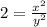
Now, it is clear that x is an even number. So, let us substitute x = 2u
Thus,
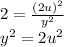
Thus,
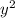 is even, which follows the fact that y is also an even number. But this is a contradiction as x and y have a common factor that is 2 but we assumed that the fraction
is even, which follows the fact that y is also an even number. But this is a contradiction as x and y have a common factor that is 2 but we assumed that the fraction
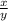 was in lowest form.
was in lowest form.
Hence,
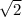 is not a rational number. But
is not a rational number. But
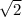 is a an irrational number.
is a an irrational number.