Answer:
2.2 µm
Step-by-step explanation:
For constructive interference, the expression is:
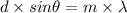
Where, m = 1, 2, .....
d is the distance between the slits.
Given wavelength = 597 nm
Angle,
 = 15.8°
= 15.8°
First bright fringe means , m = 1
So,
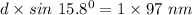
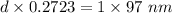
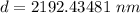
Also,
1 nm = 10⁻⁹ m
1 µm = 10⁻⁶ m
So,
1 nm = 10⁻³ nm
Thus,
Distance between slits ≅ 2.2 µm