Question

Consider the claim: If m is an even integer, then m^2+5m-1 is an odd integer.

(a.) Prove the claim using a direct proof.

(b.) State the converse. Is the converse true? Provide a proof or give a counterexample.

I have read the previous examples and am having trouble with them so please don't copy and paste a retired answer.

Answer 1

Rewriting the expression using m=2p we have:

Answer:

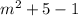`m^(2) +5 -1` is an odd integer but the converse is not true.

Explanation:

Even numbers are written as 2n where n is any integer, while odd numbers are written as 2n-1 where n is any integer.

a) To prove that
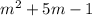`m^(2) +5m-1` is an odd integer, we have to prove that it can be written as 2n-1.

By hypothesis, m is an even integer so we will write it as 2p.

Rewriting the original expression using
`m=2p` we have:

`m^(2) +5m-1 = (2p)^(2) +5(2p)-1`

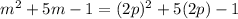
Solving the expression and factorizing it we get

`4p^(2) +10p -1 = 2(2p^(2)+5p) -1\\ \\`

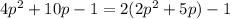
And this last expression is an expression of the form 2n-1, and therefore
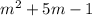`m^(2) +5m-1` is an odd integer.

b) The converse would be: if
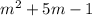`m^(2) +5m-1` is an odd integer, then m is an even integer.

We'll give a counterexample, let's make
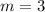`m=3`, then

`m^(2) +5m-1`

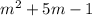
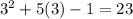`3^(2)+5(3)-1 = 23` is an odd integer but m is odd.

Therefore, the converse is not true.