Question

A ball with mass m kg is thrown upward with initial velocity 28 m/s from the roof of a building 17 m high. Neglect air resistance Use g = 9.8 m/s. Round your answers to one decimal place. (a) Find the maximum height above the ground that the ball reaches. meters (b) Assuming that the ball misses the building on the way down, find the time that it hits the ground. Fend Click If you would like to Show Work for this question: Open Show Work LINK TO TEXT

Answer 1

The ball will take 6.3 seconds to reach the maximum height and hit the ground.

Explanation:

a). When a ball was thrown upwards with an initial velocity u then maximum height achieved h will be represented by the equation

v² = u² - 2gh

where v = final velocity at the maximum height h

and g = gravitational force

Now we plug in the values in the equation

At maximum height final velocity v = 0

0 = (28)² - 2×(9.8)h

19.6h = (28)²

h =
`((28)^(2))/(19.6)`

=
`(784)/(19.6)`

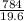
= 40 meter

B). If the ball misses the building and hits the ground then we have to find the time after which the ball hits the ground that will be

= Time to reach the maximum height + time to hit the ground from the maximum height

Time taken by the ball to reach the maximum height.

Equation to find the time will be v = u - gt

Now we plug in the values in the equation

0 = 28 - 9.8t

t =
`(28)/(9.8)`

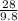
= 2.86 seconds

Now time taken by the ball to hit the ground from its maximum height.

H = ut +
`(1)/(2)* g* (t)^(2)`

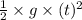
(17 + 40) = 0 +
`(1)/(2)* g* (t)^(2)`

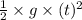
57 = 4.9(t)²

t² =
`(57)/(4.9)`

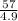
t² = 11.63

t = √(11.63)

= 3.41 seconds

Now total time taken by the ball = 2.86 + 3.41

= 6.27 seconds

≈ 6.3 seconds

Therefore, the ball will take 6.3 seconds to reach the maximum height and hit the ground.