Question

A glider moves along an air track with constant acceleration a. It is projected from the start of the track (x = 0 m) with an initial velocity of v0. At time t = 8s, it is at x = 100 cm and is moving along the track at velocity vt = − 0.15 m/s. Find the initial velocity v0 and the acceleration a.

Answer 1

vo = 0.175m/s

a = -0.040625 m/s^2

Step-by-step explanation:

To solve this problem, you will need to use the equations for constant acceleration motion:

`x = (1)/(2)at^2 +v_ot+x_o \\v_f^2 - v_o^2 = 2(x-x_o)a`

In the first equation you relate final position with the time elapsed, in the second one, you relate final velocity at any given position. In both equations, you will have both the acceleration a and the initial velocity vo as variables. We can simplify with the information we have:

1.
`x = (1)/(2)at^2 +v_ot+x_o\\0.1m = (1)/(2)a(8s)^2 +v_o(8s)+0m \\0.1 = 32a + 8v_o`

2.
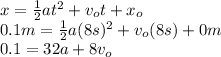
`v_f^2 - v_o^2 = 2(x-x_o)a\\(-0.15m/s)^2 - v_o^2 = 2(0.1m-0m)a\\0.0225 - v_o^2 = 0.2a\\a = (0.0225 - v_o^2)/(0.2) = 0.1125 - 5v_o^2`

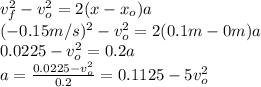
Replacing in the first equation:

`0.1 = 32(0.1125 - 5v_o^2) + 8v_o\\0.1 = 3.6 - 160v_o^2 + 8v_o\\160v_o^2 - 8v_o - 3.5 = 0`

`v_0 = (-(-8) +- √((-8)^2 - 4(160)(-3.5)))/(2(160)) \\ v_o = 0.175 m/s | -0.125 m/s`

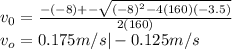
But as you are told that the ball was projected om the air track, it only makes sense for the velocity to be positive, otherwise it would have started moving outside the air track, so the real solution is 0.175m/s. Then, the acceleration would be:

`a = 0.1125 - 5v_o^2\\a = -0.040625  m/s^2`