Question

How much interest will you have to pay for a credit card balance of $1,034 that is 1 month overdue, if a 17% annual rate is charged? You will have to pay $1224.43| in interest. (Round to two decimal places.)

Answer 1

Ans. Since the annual rate is not compunded (for example, compounded monthly) you will have to pay in interest $27.41, and the total payment is $1,061.41

Explanation:

Hi, since the balance is 1 month overdue, it means that you owe 2 months of interest to this obligation, but before we start finding the interest of your credit card, first let´s find the effective monthly equivalent rate for that 17% annual interest rate.

The formula is as follows.

`r(monthly)=(1+r(annual))^{(1)/(12) }-1`

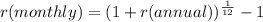
Therefore

`r(monthly)=(1+0.17)^{(1)/(12) }-1 =0.01317`

So your monthly interest rate is 1.317%. Now let´s find the amount of interests that you have to pay for 2 months. This is the formula.

`Interest=Present Value(1+r(monthly))^(n) )-PresentValue`

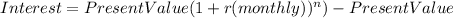
Where "n" is the period of time in months that you owe to the financial institution. The result of that is:

`Interest=1,034(1+0.01317)^(2) -1,034=24.41`

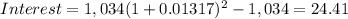
This way, interest are = $27.41 and the total amount that you will have to pay is:

`Payment=Present Value+Interest=1,034+27.41=1,061.41`

Best of luck.