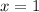Question

Solve the following logarithmic equation: In(x +31)-In(4-3x)-5In2 0 x = 2 1 points x= 0 x-0.5 ○ x=0.25 None of the above to save all

Answer 1

The solution is
`x = 1`

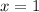
Explanation:

We have the following logarithmic properties:

`ln a + ln b = ln ab`

`ln a - ln b = ln (a)/(b)`

`n ln a = ln a^(n)`

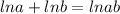
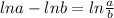
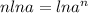
We have the following logarithmic equation:

`ln(x + 31) - ln (4-3x) - 5 ln 2 = 0`

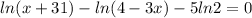
Lets simplify, and try to find properties.

`ln(x + 31) - (ln (4-3x) + 5 ln 2) = 0`

`ln(x + 31) - (ln (4-3x) + ln 2^(5)) = 0`

`ln(x + 31) - (ln (4-3x) + ln 32) = 0`

`ln(x + 31) -  ln 32*(4-3x) = 0`

`ln(x+31) - ln (128 - 96x) = 0`

`ln (x + 31)/(128 - 96x) = 0`

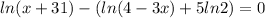
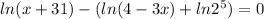
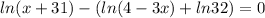
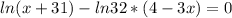
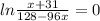
To eliminate the ln, we apply the exponential to both sides, since e and ln are inverse operations.

`e^{ln (x + 31)/(128 - 96x)} = e^(0)`

`(x + 31)/(128 - 96x) = 1`

`x + 31 = 128 - 96x`

`97x = 97`

`x = (97)/(97)`

`x = 1`

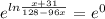
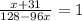
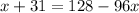
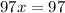
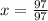
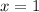
The solution is
`x = 1`