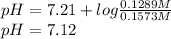Question

A buffer, consisting ofH2PO4-

andHPO42-, helps control the pH of
physiologicalfluids. Many carbonated soft drinks also use this
buffer system.What is the pH of a soft drink in which the major
bufferingredients are 6.70 g ofNaH2PO4 and
6.50g of Na2HPO4 per 355 mL
ofsolution?

Answer 1

The pH of the drink is 7.12

Step-by-step explanation:

First, we calculate the concentration of NaH₂PO₄ and Na₂HPO₄, using their molecular weight and the volume in L (355 mL= 0.355 L):

[NaH₂PO₄] =
`(6.70g)/(0.355L*120g/mol)= 0.1573 M`

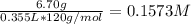
[Na₂HPO₄] =
`(6.50g)/(0.355L*142g/mol) = 0.1289 M`

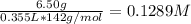
Now we calculate the pH of the solution, keeping in mind the equilibrium:

• H₂PO₄⁻ ↔ HPO₄⁻² + H⁺

From literature, we know that the pka for the previous equilibrium is 7.21

The equation that gives us the pH of a buffer solution is the Henderson–Hasselbalch equation:

pH = pka +
`log([HPO4^(-2) ])/([H2PO4^(-) ])`

Replacing in the equation the data we know gives us:

`pH=7.21+log(0.1289M)/(0.1573M) \\pH=7.12`