Answer:
The function a (t) is a vector function composed of the component functions
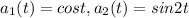 and
and
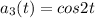 . How
. How
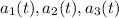 are infinitely derivable functions in R, so they are regular functions in R.
are infinitely derivable functions in R, so they are regular functions in R.
Now, for
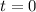 , you have to
, you have to
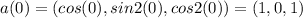 . How the functions
. How the functions
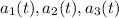 are periodic functions with period
are periodic functions with period
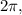 the vector function
the vector function
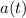 will take the same point
will take the same point
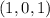 at
at
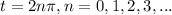 then the vector function is auto-intercepted
then the vector function is auto-intercepted
Explanation: