Answer with Step-by-step explanation:
We are given that a statement ''If I have the disease , then I will test positive.''
Let p:I have the disease.
q:I will test positive.
a.Converse :

''If I will test positive, then I have the disease''.
b.Inverse :
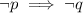
''If I have not the disease, then I will not test positive.''
c. Contrapositive:
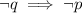
''If I will not test positive, then I have not the disease''.
d.Disjunction:p or q=

''I have the disease or I will test positive''.
e.Negation :If p is true then its negation is p is false.
Negation of conditional statement is equivalent to
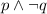
I have disease and I will not test positive.