Question

.Consider the following sine wave: s(t) = 4sin(2π3t + π)

a.What is the amplitude?

b.What is the frequency?

c.What is the phase?

Answer 1

1) Amplitude = 4

2) Frequency =
`1Hz`

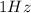
3) Initial phase =
`\pi`

Step-by-step explanation:

The general equation of wave is

`y(t)=Asin(\omega t+\phi )`

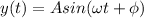
where

A is the amplitude of the wave

`\omega` is the angular frequency of the wave

`\phi` is the initial phase of the wave

The given wave function is

`s(t)=4sin(2\pi t+\pi )`

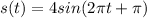
Comparing with the standard function we get

1) Amplitude = 4

2) Frequency =
`(\omega )/(2\pi )=(2\pi )/(2\pi )=1Hz`

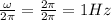
3) Initial phase =
`\pi`

Answer 2

a. 4

b. 3

c. pi

Step-by-step explanation:

Generic formula of a sine wave: s(t) = Amp * sin ( 2*pi*freq*t + phase)

where, Amp => Amplitude

freq => frequency

phase => phase

Given sine wave: s(t) = 4sin(2π3t + π)

Comparing it with the generic form , we can identify that :

a. Amplitude : 4

b. Frequency : 3

c. Phase : pi

Amplitude measures peak displacement from origin, Frequency is the number of cycles per second and phase is the relative positioning of the wave with respect to the origin.