Question

A 1.8-kg block is released from rest at the top of a rough 45° inclined plane. As the block slides down the incline, its acceleration is 2.0 m/s, down the incline. Determine the magnitude of the force of friction acting on the block. a. 16.1 N b. 8.9 N c. 12.5 N d. 2.3 N e. 17.6N

Answer 1

Ff= 8.9N:Force of friction acting on the block.

Step-by-step explanation

Box kinetics: in x₁-y₁ :We apply the second law of Newton

∑Fx₁=ma : second law of Newton Formula (1)

Where:

∑Fx₁:algebraic sum of forces in the direction of x1, positive in the direction of movement of the block, which is down and negative in the direction opposite to the movement of the block

m: is the mass of the block

The x₁ axis coincides with the plane of sliding of the block, that is, the x₁ axis forms 45 degrees with the horizontal

The total weight (W) of the block is in the vertical direction and the tip of the vector down and its magnitude is calculated as follows:

W=m*g

Where:

m: is the mass of the block

g: is the acceleration due to gravity

Calculation of the weight in the direction x₁

Wx₁=Wcos45°= m*g*cos 45 Equation( 1)

Data

m=1.8kg

g=9.8 m/s²

a=2m/s

Wx₁=m*g*cos 45°= 1.8*9.8 *
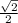`(√(2) )/(2)`= 12.47 N

Friction force (Ff ) calculation

We apply formula (1)

∑Fx₁=m*a

Wx₁ - Ff= m*a

Ff=Wx₁ - m*a

We replace data

Ff= 12.47 - 1.8*2 =8.87

Ff= 8.9N