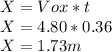Answer:
a) 3.56m/s
b) 1.73m
Step-by-step explanation:
We have to treat this as a parabolic motion problem:
we will use the next formulas:
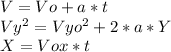
we first have to calculate the initial velocity of the basketball player:

the final velocity is zero when he reaches the maximun height.
To answer the second part we need to obtain the time to reach the maximun height, so:
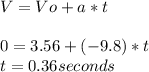
Now having that time, let's find the distance on the X axis, the X axis behaves as constant velocity movement, so: