Question

A net external nonconservative force does positive work on

aparticle, and both its kinetic and potential energies change.
What,if anything, can you conclude about
(a) the change in the particle's total mechanical energy and
(b) the individual changes in the kinetic and
potentialenergies?
Justify your answers.

Answer 1

Answer with Explanation:

From work energy theorem we have

`\Delta Energy=\int F.ds`

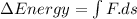
Now since it is given that the work done on the object by the force is positive hence we conclude that the term on the right hand of the above relation is positive hence
`\Delta Energy>0`

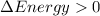
Part a)

Hence we conclude that the mechanical energy of the particle will increase.

Part b) Since the mechanical energy of the particle is the sum of it's kinetic and potential energies, we can write

`\Delta K.E+\Delta P.E=\Delta E\\\\\therefore \Delta K.E+\Delta P.E>0`

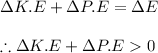
Now since the sum of the 2 energies ( Kinetic and potential ) is positive we cannot be conclusive of the individual values since 2 cases may arise:

1) Kinetic energy increases while as potential energy decreases.

2) Potential energy increases while as kinetic energy decreases.

Hence these two cases are possible and we cannot find using only the given information which case will hold

Hence no conclusion can be formed regarding the individual energies.