Question

Find the roots of the equation f(x) = x3 - 0.2589x2 + 0.02262x -0.001122 = 0

Answer 1

The root of the equation
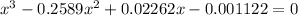`x^3-0.2589x^(2)+0.02262x-0.001122=0` is x ≈ 0.162035

Explanation:

To find the roots of the equation
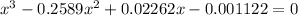`x^3-0.2589x^(2)+0.02262x-0.001122=0` you can use the Newton-Raphson method.

It is a way to find a good approximation for the root of a real-valued function f(x) = 0. The method starts with a function f(x) defined over the real numbers, the function derivative f', and an initial guess
`x_(0)` for a root of the function. It uses the idea that a continuous and differentiable function can be approximated by a straight line tangent to it.

This is the expression that we need to use

`x_(n+1)=x_(n) -(f(x_(n)))/(f(x_(n))')`

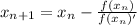
For the information given:

`f(x) = x^3-0.2589x^(2)+0.02262x-0.001122=0\\f(x)'=3x^2-0.5178x+0.02262`

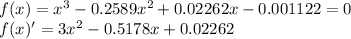
For the initial value
`x_(0)` you can choose
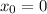`x_(0)=0` although you can choose any value that you want.

So for approximation
`x_(1)`

`x_(1)=x_(0)-(f(x_(0)))/(f(x_(0))') \\x_(1)=0-(0^3-0.2589\cdot0^2+0.02262\cdot 0-0.001122)/(3\cdot 0^2-0.5178\cdot 0+0.02262) \\x_(1)=0.0496021`

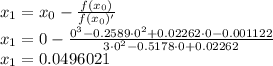
Next, with
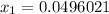`x_(1)=0.0496021` you put it into the equation

`f(0.0496021)=(0.0496021)^3-0.2589\cdot (0.0496021)^2+0.02262\cdot 0.0496021-0.001122 = -0.0005150`, you can see that this value is close to 0 but we need to refine our solution.

For approximation
`x_(2)`

`x_(2)=x_(1)-(f(x_(1)))/(f(x_(1))') \\x_(1)=0-(0.0496021^3-0.2589\cdot 0.0496021^2+0.02262\cdot 0.0496021-0.001122)/(3\cdot 0.0496021^2-0.5178\cdot 0.0496021+0.02262) \\x_(1)=0.168883`

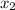
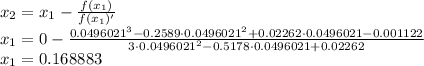
Again we put
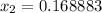`x_(2)=0.168883` into the equation

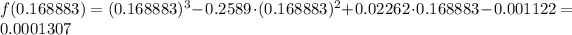`f(0.168883)=(0.168883)^3-0.2589\cdot (0.168883)^2+0.02262\cdot 0.168883-0.001122=0.0001307` this value is close to 0 but again we need to refine our solution.

We can summarize this process in the following table.

The approximation
`x_(5)` gives you the root of the equation.

When you plot the equation you find that only have one real root and is approximate to the value found.