Answer:
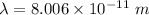
Step-by-step explanation:
Given that,
The speed of an electron,
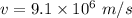
We need to find the wavelength of this electron. It can be calculated using De -broglie wavelength concept as :
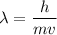
h is the Planck's constant
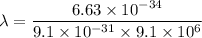
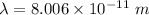
So, the wavelength of the electron is
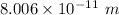 . Hence, this is the required solution.
. Hence, this is the required solution.