Question

A mixture of water and ethanol has a total mass of 100 kg. The

mole fraction of water is 0.752. what is the mass of ethanol in
this mixture, in kg?

Answer 1

45.8 kg

Step-by-step explanation:

Given that the mole fraction of water = 0.752

For a binary system,

The mole fraction of water + The mole fraction of ethanol = 1

So,

The mole fraction of ethanol = 0.248

Given that the total mass = 100 kg

Let the mass of ethanol = x kg

The mass of water = 100 - x kg

The formula for the calculation of moles is shown below:

`moles = (Mass\ taken)/(Molar\ mass)`

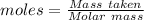
Molar mass of ethanol = 46.07 g/mol

Molar mass of water = 18 g/mol

Also, 1 g = 10⁻³ kg

So,

Molar mass of ethanol = 46 ×10⁻³ kg/mol

Molar mass of water = 18 ×10⁻³ kg/mol

Moles of ethanol = x / 46 ×10⁻³ moles

Moles of water = (100 - x) / 18 ×10⁻³ moles

So, according to definition of mole fraction:

`Mole\ fraction\ of\ ethanol=\frac {n_(ethanol)}{n_(ethanol)+n_(water)}`

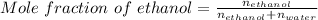
Applying values as:

`0.248=\frac {\frac {x}{46* 10^(-3)}}{\frac {x}{46* 10^(-3)}+\frac {(100-x)}{18* 10^(-3)}}`

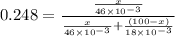
Solving for x, we get

x = 45.8 kg

Mass of ethanol in mixture = 45.8 kg