Question

Consider a particle moving around a circle with a radius of 38cm. It rotates from 10 degrees to 100 degrees in 11 seconds. Calculate the instantaneous velocity of the particle.

Answer 1

Explanation:

Given that,

Radius of circle, r = 38 cm = 0.38 m

It rotates form 10 degrees to 100 degrees in 11 seconds i.e.

`\theta_i=10^(\circ)=0.174\ rad`

`\theta_f=100^(\circ)=1.74\ rad`

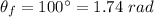
Let
`\omega` is the angular velocity of the particle such that,
`\omega=(\omega_f-\omega_i)/(t)`

`\omega=(1.74-0.174)/(11)`

`\omega=0.142\ rad/s`

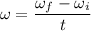
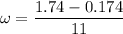
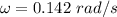
We need to find the instantaneous velocity of the particle. The relation between the angular velocity and the linear velocity is given by :

`v=r* \omega`

`v=0.38* 0.142`

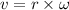
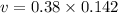
v = 0.053 m/s

So, the instantaneous velocity of the particle is 0.053 m/s. Hence, this is the required solution.