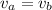Question

A student at the top of a building of height h throws ball A straight upward with speed v0 (3 m/s) and throws ball B straight downward with the same initial speed. A. Compare the balls’ accelerations, both direction, and magnitude, immediately after they leave her hand. Is one acceleration larger than the other? Or are the magnitudes equal? B. Compare the final speeds of the balls as they reach the ground. Is one larger than the other? Or are they equal?

Answer 1

Answer:same

Step-by-step explanation:

Given

ball A initial velocity=3 m/s(upward)

Ball B initial velocity=3 m/s (downward)

Acceleration on both the balls will be acceleration due to gravity which will be downward in direction

Both acceleration is equal

For ball A

maximum height reached is
`h_1=(3^2)/(2g)`

After that it starts to move downwards

thus ball have to travel a distance of h_1+h(building height)

so ball A final velocity when it reaches the ground is

`v_a^2=2g\left ( h_1+h\right )`

`v_a^2=2g\left ( 0.458+h\right )`

`v_a=√(2g\left ( 0.458+h\right ))`

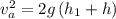
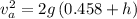
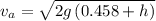
For ball b

`v_b^2-\left ( 3\right )^2=2g\left ( h\right )`

`v_b^2=2g\left ( (3^2)/(2g)+h\right )`

`v_b=√(2g\left ( 0.458+h\right ))`

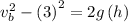
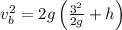
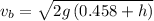
thus
`v_a=v_b`