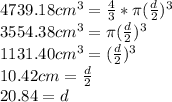Question

A boy on the beach holds a spherical balloon filled with air. At 7:00 am, the temperature on the beach is 35°F and the balloon has a diameter of 20 cm. Six hours later, the outside temperature is 100°F. Assume that the air is an ideal gas, that the atmospheric pressure remains constant, and that no air was lost or added to the balloon. What is the final diameter of the balloon (in cm)?

Answer 1

The final diameter of the balloon is 20.84 cm.

Step-by-step explanation:

To answer this problem, because both the number of moles (because no air was lost or added to the balloon) and the pressure remain constant, we can use Charles' law, or the law of volumes:

V₁T₂=V₂T₁

Where V is Volume (in L) and T is temperature (in K). The subscripts 1 and 2 refer to different states of the gas: for this problem, let's say that ₁ refers to the state of the gas at 7:00 am and that ₂ refers to the state 6 hours later.

To calculate the volume occupied by the gas we use the formula for the volume of a sphere:

`V=(4)/(3)*\pi  ((d)/(2))^(3)`

Thus the volume of the balloon at 7:00 am is 4188.79 cm³

Then we convert °F into K:

• (35°F + 459.67) * 5/9 = 274.82 K = T₁
• (100°F + 459.67) * 5/9 = 310.93 K = T₂

Now we use Charles' law to calculate V₂:

V₂=V₁T₂/T₁

V₂=
`(4188.79cm^(3)*310.93K)/(274.82 K)=4739.18cm^(3)`

Lastly we calculate the final diameter of the balloon:

`4739.18cm^(3)=(4)/(3)*\pi  ((d)/(2))^(3)\\3554.38cm^(3)=\pi  ((d)/(2))^(3)\\1131.40cm^(3)=((d)/(2))^(3)\\10.42cm=(d)/(2)\\20.84=d`