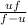Answer:
see explanation
Explanation:
Multiply through by the lowest common multiple of u, v and f, that is uvf
uvf ×
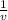 + uvf ×
+ uvf ×
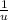 = uvf ×
= uvf ×
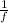 , that is
, that is
uf + vf = uv ← factor out f on the left side → (1)
f(u + v) = uv ← divide both sides by (u + v)
f =
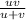
(b)
Using line (1)
uf + vf = uv ( subtract uv from both sides )
uf + vf - uv = 0 ( subtract uf from both sides )
vf - uv = - uf ← factor out v on the left side
v(f - u) = - uf ← divide both sides by (f - u)
v = -