Question

Is the set of all 2x2 matrices such that det(A)=0 a subspace of the vector space of all 2x2 matrices?

Answer 1

The answer is no: the set of all 2x2 matrices such that det(A)=0 is not a subspace of the vector space of all 2x2 matrices.

Explanation:

In order for a set of matrices to be a subspace of all 2x2 matrices, three conditions must be satisfied:

1) That the set is not empty.

2) If A and B are both 2x2 matrices with zero determinant then the matrix A+B should also be a matrix with zero determinant.

3) The determinant of c*A, where "c" is any complex number and A is any matrix of the set, should be zero.

1)

The first condition is satisfied by the set of all 2x2 matrices such that det(A)=0, since there are plenty 2x2 matrices with zero determinant.

2)

The second condition is not satisfied, since from the determinant properties, we know that:

`det(A+B)\geq det(a)+det(B)`

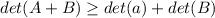
The equality might hold, but it is not a general characteristic. For example, if we consider the following matrices:

`A = \left[\begin{array}{cc}1&0\\0&0\end{array}\right], \quad B = \left[\begin{array}{cc}0&0\\0&1\end{array}\right]`

We can easily check that the determinant of both matrices is zero, nevertheless the determinant of the sum is different than zero.

Therefore, the set of all 2x2 matrices such that det(A)=0 is not a subspace of the vector space of all 2x2 matrices.