Question

April shoots an arrow upward into the air at a speed of 64 feet per second from a platform that is 11 feet high. The height of the arrow is given by the function h(t) = -16t2 + 64t + 11, where t is the time is seconds. What is the maximum height of the arrow?

Answer 1

Maximum height of the arrow is 203 feets

Explanation:

It is given that,

The height of the arrow as a function of time t is given by :

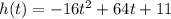`h(t)=-16t^2+64t+11`..........(1)

t is in seconds

We need to find the maximum height of the arrow. For maximum height differentiating equation (1) wrt t as :

`(dh(t))/(dt)=0`

`(d(-16t^2+64t+11))/(dt)=0`

`-32t+64=0`

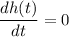
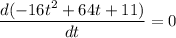
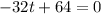
t = 2 seconds

Put the value of t in equation (1) as :

`h(t)=-16(2)^2+64(2)+11`

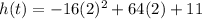
h(t) = 203 feet

So, the maximum height reached by the arrow is 203 feet. Hence, this is the required solution.