Question

Heat transfer through solid composites depend on (Lower composite heat conductivity • higher composite heat conductivity • Lower composite heat capacity • higher composite heat capacity

Answer 1

Answer: Option (b) is the correct answer.

Step-by-step explanation:

According to Fourier's equation,

Q =
`kA((\Delta T)/(\Delta x))`

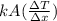
Also,
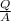`(Q)/(A)` = q

So, q =
`k((\Delta T)/(\Delta x))`

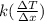
where, Q = quantity of heat transferred

A = area of heat transferred

q = rate of heat transfer

`\Delta T` = change in temperature

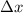`\Delta x` = thickness

k = thermal conductivity of the solid material

Since rate of heat transfer is directly proportional to k, which is also known as thermal conductivity.

Therefore, it means that higher is the value of k higher will be rate of heat transfer (q). And, lower is the value of k lower will be the rate of heat transfer (q).

Thus, we can conclude that heat transfer through solid composites depend on higher composite heat conductivity.