Question

Let S = {a, b, c). Find the following:

a) the number of reflexive relations on S

b)the number of reflexive and symmetric relations on S

Answer 1

The number of reflexive relations on S is 64.

The number of reflexive and symmetric relations on S is 8.

Explanation:

Consider the provided set S = {a, b, c}.

The number of elements in the provided set is 3.

Part (a) the number of reflexive relations on S

To calculate the number of reflexive relation on S we can use the formula as shown:

Total number of Reflexive Relations on a set:
`2^(n(n-1))`.

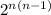Where, n is the number of elements.

In the provided set we have 3 elements, so substitute the value of n in the above formula:

`2^(3(3-1))`

`2^(3(2))`

`2^(6)`

`64`

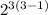
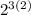
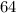
Hence, the number of reflexive relations on S is 64.

Part(b) The number of reflexive and symmetric relations on S.

To calculate the number of reflexive and symmetric relation on S we can use the formula as shown:

Total number of Reflexive and symmetric Relations on a set:
`2^{(n(n-1))/(2)}`.

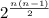Where, n is the number of elements.

In the provided set we have 3 elements, so substitute the value of n in the above formula:

`2^{(3(3-1))/(2)}`

`2^{(3(2))/(2)}`

`2^{(6)/(2)}`

`2^(3)`

`8`

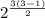
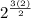
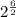
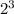
Hence, the number of reflexive and symmetric relations on S is 8.