1 Answer

Asetti Sri Harsha · Answer 1 · 2020-07-28T06:35:00+0000

Answer:

Explanation:

If we assume that
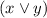$[(x \vee y) \wedge (x \rightarrow z) \wedge (\\eg z)]$ is true, then:

$(x \vee y)$ is true

$(x \rightarrow z)$ is true

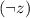$(\\eg z)$ is true

If
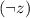$(\\eg z)$ is true, then
is false.

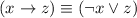$(x \rightarrow z) \equiv (\\eg x \vee z)$ , since
$(x \rightarrow z)$ is true, then
$(\\eg x \vee z)$ is true

If
is false and
$(\\eg x \vee z)$ is true, then
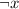$\\eg x$ is true.

If
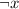$\\eg x$ is true, then
is false, as
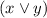$(x \vee y)$ is true and
is false, then
is true.

Conclusion
it's true.

Please log in or register to add a comment.