Answer:
97
Explanation:
We are asked to find the size of sample to be 95% confident that the error in psychologist estimate of mean reaction time will not exceed 0.01 seconds.
We will use following formula to solve our given problem.
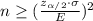 , where,
, where,
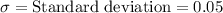 ,
,
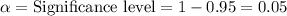 ,
,
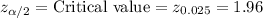 .
.
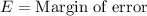
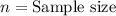
Substitute given values:
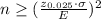
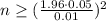
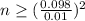
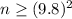
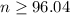
Therefore, the sample size must be 97 in order to be 95% confident that the error in his estimate of mean reaction time will not exceed 0.01 seconds.