Question

A ball is thrown upward at initial velocity of 20 m/s at the edge of a cliff 150 m high. 1. Find time it takes to reach the top of the path.2. Find total time it takes to reach bottom.3. Find final velocity at bottom.

Answer 1

1. 2 second

2. 7.83 second

3. 58.31 m/s

Step-by-step explanation:

initial velocity, u = 20 m/s

g = 10 m/s^2

1. Let it takes time t1 to reach to maximum height.

At maximum height the final velocity of the ball is zero.

use first equation of motion, we get

v = u + at

0 = 20 - 10 t1

t1 = 2 second

Thus, the time taken to reach to maximum height is 2 second.

2. The maximum height above the cliff is h

Use third equation of motion

`v^(2)=u^(2)+2as`

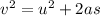
0 = 20 x 20 - 2 x 10 x h

400 = 20 h

h = 20 m

The total height is 20 + 150 = 170 m

let the time taken by the ball to reach to bottom from maximum height is t2.

use third equation of motion

`s = ut + (1)/(2)at^(2)`

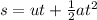
170 = 0 + 0.5 x 10 x t2^2

t2 = 5.83 second

thus, the total time to reach to bottom, t = t1 + t2 = 2 + 5.83 = 7.83 second.

3. Let v be the velocity with which the ball strikes the ground.

Use third equation of motion, we get

`v^(2)=u^(2)+2as`

`v^(2)=0^(2)+2* 10 * 170`

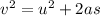
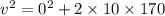
v = 58.31 m/s

Thus, the ball reaches the ground with velocity of 58.31 m/s.