Question

An unknown radioactive element decays into non-radioactive substances. In 30 days the radioactivity of a sample decreases by 12%. When will a sample of 50 mg decay to 10 mg? Round your final answer to 1 decimal place.

Answer 1

Time to decay will be 377.7 days.

Explanation:

Decay of an radioactive element is represented by the formula

`A_(t)=A_(0)e^(-kt)`

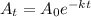
where
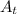`A_(t)` = Amount after t days

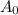`A_(0)` = Initial amount

t = duration for the decay

k = decay constant

Now we plug in the values in the formula

`(1-0.12)x=xe^(-30k)`

`(0.88)x=xe^(-30k)`

`0.88=e^(-30k)`

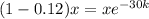
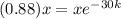
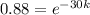
Now we take natural log on both the sides

ln(0.88) =
`ln(e)^(-30k)`

ln(0.88) = -30k(lne)

-30k = -0.1278

k =
`(.1278)/(30)`

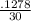
k =
`4.261* 10^(-3)`

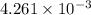
Now we have to calculate the duration for the decay of 50 mg sample to 10 mg.

`A_(t)=A_(0)e^(-kt)`

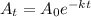
We plug in the values in the formula

10 = 50
`e^{-4.261* 10^(-3)* t}`

`e^{-4.261* 10^(-3)* t}=(10)/(50)`

`e^{-4.261* 10^(-3)* t}=0.2`

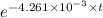
We take (ln) on both the sides

`ln(e^{-4.261* 10^(-3)* t})=ln(0.2)`

`-4.261* 10^(-3)* t=-1.6094`

t =
`(1.6094)/(4.261* 10^(-3) )`

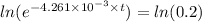
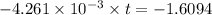
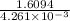
t = 0.37771×10³

t = 377.7 days

Therefore, time for decay will be 377.7 days.