Answer:
(a)
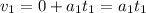 .
.
(b)
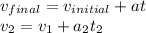
(c)

Step-by-step explanation:
Part (a):
To find an expression for the rocket's speed
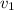 at time
at time
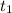 , we use the constant acceleration model, which relates these variables with the expression:
, we use the constant acceleration model, which relates these variables with the expression:
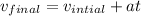 . In this case, the initial velocity is null, because accelerates from rest. So, we take all values of the first interval, and we replace it to find the expression:
. In this case, the initial velocity is null, because accelerates from rest. So, we take all values of the first interval, and we replace it to find the expression:
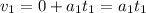 . (expression for the first interval).
. (expression for the first interval).
Part (b):
Then, we do the same process to find the expression of the second interval, we just replace the variables given:
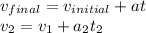
In this case, you can notice that the initial velocity used is the one we obtain from the first interval, because the end of the first period is the beginning of the second period.
Part (c):
To calculate the total distance we have to sum the distance covered during the two intervals, that it's translated as:
 .
.
Then, we use this equation to replace in each distance:
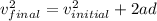 .
.
Isolating d we have:
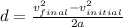 .
.
Now, we apply the equation to each interval to obtain
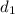 and
and
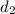 :
:
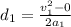 .
.
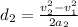 .
.
Before calculating the total distance, we need to know the magnitude of each speed.

![v_(1)=(67)(39)=[tex]v_(2)=v_(1)+a_(2) t_(2)= 2613(m)/(s^(2))+34(m)/(s^(2))(49sec)=4279(m)/(s)](https://img.qammunity.org/2020/formulas/physics/college/vqurf551syb374uvddx09krr2w71nb2or7.png) [/tex]
[/tex]
At last, we use all values known to calculate the total distance:

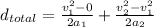 .
.

Therefore, the total distance traveled until the ends of the second period is
 . The rocket is in the Thermosphere.
. The rocket is in the Thermosphere.