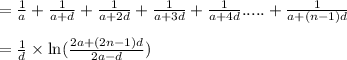Question

Find the following area of the following region, expressing your result in terms of the positive integer n\geq2.

The region bounded by f(x)=x and g(x)= x1/n , for x\geq 0

The area of the region in terms of n is_____???

Answer 1

The two region under whose we have to find area is

f(x)=x

`g(x)=x^{(1)/(n)}\\\\x \geq 0\\\\n\geq 2`

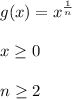
The Point of Intersection of two curves is always , x=0 and x=1.

Area of the Region

=Area under the line - Area Under the curve g(x), when n take different value, that is ≥2.

`\rightarrow[- \int\limits^1_0 {x} \, dx + \int\limits^1_0 {x^{(1)/(2)} \, dx]+[ -\int\limits^1_0 {x} \, dx + \int\limits^1_0 {x^{(1)/(3)} \, dx]+[ -\int\limits^1_0 {x} \, dx + \int\limits^1_0 {x^{(1)/(4)} \, dx]+[ -\int\limits^1_0 {x} \, dx + \int\limits^1_0 {x^{(1)/(5)} \, dx]+......`

`=\int\limits^1_0({x^{(1)/(2)}+x^{(1)/(3)}+x^{(1)/(4)}+x^{(1)/(5)}+.......+x^{(1)/(200)}}) \, dx -\int\limits^1_0 ({x}+{x}+{x}+{x}...........+200\text{times}) \, dx`

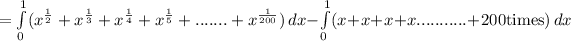
When, n=200, the first quadrant is completely occupied by the curve

`g(x)=x^{(1)/(n)},x\geq 0\\\\2\leq n \leq 200`

`=\int\limits^1_0{x^{(1)/(n)} \, dx=\frac{n* x^{((1)/(n)+1)}}{n+1}\left \{ {{x=1} \atop {x=0}} \right.}\\\\= (n)/(n+1)\\\\\int\limits^1_0{x^(n) \, dx=(x^(n+1))/(n+1)\left \{ {{x=1} \atop {x=0}} \right.}\\\\=(1)/(n+1)`

`=(2)/(3)+(3)/(4)+(4)/(5)+...........+(200)/(201)-199 * (1)/(2)\\\\=1-(1)/(3)+1-(1)/(4)+1-(1)/(5)+...........+1-(1)/(201)-99.5\\\\=199-99.5+(1)/(3)+(1)/(4)+(1)/(5)+...........+(1)/(201)\\\\=99.5+1+(1)/(2)+(1)/(3)+(1)/(4)+(1)/(5)+...........+(1)/(201)-1-(1)/(2)\\\\=98+(1)/(d) *\ln((2a+(2n-1)d)/(2a-d))\\\\=98+\ln((2 * 1+(2* 201-1)* 1)/(2* 1-1))\\\\=98+\ln 403\\\\=98+6({\text{approx}})\\\\=104 \text{square units}`

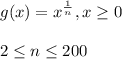
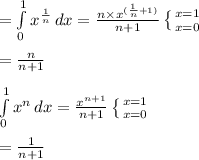
Sum of n terms of Harmonic Progression is

`=(1)/(a)+(1)/(a+d)+(1)/(a+2d)+(1)/(a+3d)+(1)/(a+4d).....+(1)/(a+(n-1)d)\\\\=(1)/(d) * \ln((2a+(2n-1)d)/(2a-d))`