Question

How many times greater is the area circle 1( radius 12) of than the area circle 2( radius 4) of ​?

Answer 1

The area of circle 1 is 9 times greater than area of circle 2.

Explanation:

Given that:

Radius of circle 1 = 12

Area of circle 1 = πr²

Area of circle 1 =
`3.14*(12)^2 = 3.14*144`

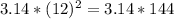
Area of circle 1 = 452.16

Radius of circle 2 = 4

Area of circle 2 =
`3.14*(4)^2 = 3.14*16`

Area of circle 2 = 50.24

Let,

x be the number of times circle 1 is bigger than circle 2.

Area circle 1 = x * Area circle 2

`(452.16)/(50.24)=(50.24x)/(50.24)\\\\x=9`

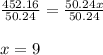
Hence,

The area of circle 1 is 9 times greater than area of circle 2.