Question

An infinitely long line of charge has a linear charge density of 7.50×10^−12 C/m . A proton is at distance 14.5 cm from the line and is moving directly toward the line with speed 3000 m/s . How close does the proton get to the line of charge? Express your answer in meters.

Answer 1

10.22 cm

Step-by-step explanation:

linear charge density, λ = 7.5 x 10^-12 C/m

distance from line, r = 14.5 cm = 0.145 m

initial speed, u = 3000 m/s

final speed, v = 0 m/s

charge on proton, q = 1.6 x 10^-19 C

mass of proton, m = 1.67 x 10^-27 kg

Let the closest distance of proton is r'.

The potential due t a line charge at a distance r' is given by

`V=-2K\lambda ln\left ((r')/(r)  \right )`

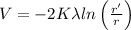
where, K = 9 x 10^9 Nm^2/C^2

W = q V

By use of work energy theorem

Work = change in kinetic energy

`qV = 0.5m(u^(2)-v^(2))`

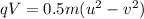
By substituting the values, we get

`V=(mu^(2))/(2q)`

`-2K\lambda ln\left ( (r')/(r) \right )=(mu^(2))/(2q)`

`- ln\left ( (r')/(r) \right )=(mu^(2))/(4Kq\lambda )`

`- ln\left ( (r')/(r) \right )=(1.67 * 10^(-27)* 3000* 3000)/(4* 9* 10^(9)* 1.6* 10^(-19)* 7.5* 10^(-12) )`

`- ln\left ( (r')/(r) \right )=0.35`

`(r')/(r) =e^(-0.35)`

`(r')/(r) =0.7047`

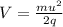
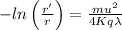
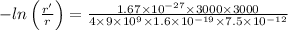
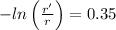
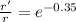
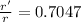
r' = 14.5 x 0.7047 = 10.22 cm