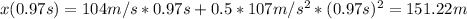Question

An electron with speed of 104 m/s enters a ""forbidden"" region where an electric force tries to push it back along its path with a constant acceleration of 107 m/s2 . How far will the electron go into the ""forbidden"" region? How long will it be in that region?

Answer 1

The distance travelled is 151.22m and it took 0.97s

Step-by-step explanation:

Well, this is an ARM problem, so we will need the following formulas

`x(t)=x_(0) +v_(0) *(t-t_(0) )+0.5*a*(t-t_(0) )^(2)`

`v(t)=v_(0) +a*(t-t_(0) )`

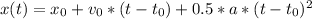
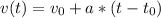
where
`x_(0)` is the initial position (we can assume is zero),
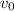`v_(0)` is the initial speed of 104 m/s,
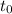`t_(0)` is the initial time (we also assume is zero), a is the acceleration of 107 m/s2, v is speed, x is position and t is time.

Now that we have the formulas, we know that when the electron stops it has no speed. Then we calculate how much time it takes to stop.

`0=104m/s-107m/s^(2) *t\\t=0.97s`

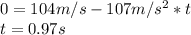
Finally, we calculate the distance travelled in this time

`x(0.97s)=104m/s*0.97s+0.5*107m/s^(2)*(0.97s)^(2)=151.22m`

Answer 2

Part a)

`d = 5 m`

Part b)

`T = 2* 10^(-3) s`

Step-by-step explanation:

Part a)

The electron will move in this forbidden region till its speed will become zero

So here we will have

`v_f = 0`

`v_i = 10^4 m/s`

also its deceleration is given as

`a = - 10^7 m/s^2`

so we will have

`v_f^2 - v_i^2 = 2 a d`

`0 - (10^4)^2 = 2(-10^7) d`

`d = 5 m`

Part b)

Now the time till its speed is zero

`v_f - v_i = at`

`0 - 10^4 = -10^7 t`

`t = 10^(-3) s`

so total time that it will be in the region is given as

`T = 2 t`

`T = 2* 10^(-3) s`