Answer:
7 groups, 3 boys and 8 girls
Explanation:
Let total number of groups be

and total hikers in one group be

if number of girls and boys in every group is same, then
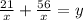
 ....(1)
....(1)
from (1)
 will either be 11 or 7
will either be 11 or 7
for
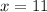 the values won't be real.
the values won't be real.
For
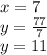
so there will be 7 groups with 11 hikers in each groups and every group will have
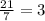 boys and
boys and
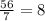 girls
girls