Question

Ray’s Satellite Emporium wishes to determine the optimal order size for its best-selling satellite dish (Model TS111). Ray has estimated the monthly demand for this model to be 230 units. This model costs Ray $396 to purchase from his supplier. His annual cost to carry inventory is 10% and he estimates that orders cost $38 to process. If Ray used an order quantity of 2000 instead of the optimal order quantity, how much money would he be wasting each year?

Answer 1

It waster $74,941.2‬ per year

Step-by-step explanation:

The procedure is as follow:

1. We calcualte the Economic order Quantity
2. Then we calculatethe cost for EOQ and current order size
3. compare to know the loss for inefficiency in inventory

1.- EOQ

`Q_(opt) = \sqrt{(2DS)/(H)}`

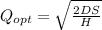
D = annual demand 230 units x 12 month = 2,760

S= setup cost = ordering cost = 38

H= Holding Cost= 10% of unit cost 39.60

`Q_(opt) = \sqrt{(2*2760*38)/(39.6)}`

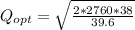
EOQ = 72.78028371 = 73

2.- Calculate Cost:

EOQ cost:

orders 2,760 / 73 = 37.80 = 38 order x $38 each = $1,444

holding cost: 73 x 39.6 = $2,890.8

Total: 1,444 + 2,890.8 = 4,334.8

Current Cost:

orders: 2,760 / 2,000 = 1.* = 2 order per year x $38 each = $76

holding cost: 2,000 x 39.6 = 79.200‬

Total 79,200 + 76 = 79,276

3.- Difference:

79,276 - 4,334.8 = 74,941.2‬